वर्ग, चतुर्भुज का एक प्रकार है जिसमे सभी भुजाएँ एक दुसरें से समनान्तर होते है. Varg Ka Kshetrafal वर्ग के इकाइयों की संख्या के रूप परिभाषित किया जाता है. क्योंकि यह वर्ग को एक प्रकार से भरने का कार्य करता है. अर्थात, यह वर्ग के किसी भी आकृति के अंदर स्थिर समतल क्षेत्र को परिभाषित करता है.
सामान्यतः वर्ग का क्षेत्रफल का माप हमेशा वर्ग इकाई में किया जाता है. जैसे, cm2, m2 आदि. क्षेत्रफल की गणना, वर्गों, आयतों, वृत्त, त्रिकोण आदि का फार्मूला पहले से ही निर्दिधारित है. लेकिन यहाँ वैसे फार्मूला का चर्चा किया जाएगा जो एग्जाम के लिए आवश्यक हो, तथा उससे प्रश्न भी पूछा जाता हो.
वर्ग की परिभाषा
गणितज्ञों के विचारधारा के ज्यामिति के अनुसार यदि किसी चतुर्भुज की चारों भुजाएं बराबर हों और चारो कोण समकोण हों तो उस चतुर्भुज को वर्ग कहते है.
गणित में Varg Ka Kshetrafal का महत्व सबसे अधिक होता है. क्योंकि, class 6 से लेकर class 12 तक इससे प्रश्न पूछा जाता है, साथ ही इसका दैनिक जीवन में भी प्रयोग होता है. इसलिए, आवश्यक है कि वर्ग का क्षेत्रफल फार्मूला का अध्ययन अलग-अलग रूप में करे.
वर्ग का क्षेत्रफल क्या है?
Varg का क्षेत्रफल किसी वस्तु द्वारा कवर किया गया वह स्थान है जिसमे आकृति अपना एक निश्चित स्थान रखती है. एक वर्ग के क्षेत्रफल को मापते समय, केवल इसके भुजाओं की लंबाई पर विचार किया जाता है. क्योंकि वर्ग के सभी पक्ष समान होते हैं. इसलिए, इसका क्षेत्रफल भुजाओं के वर्ग के बराबर होता है.
सामान्यतः Varg Ka Kshetrafal भुजाओं से गुणा करके ज्ञात किया जाता है. लेकिन कई स्थिति में क्षेत्रफल तो दिया होता है. लेकिन भुजाएँ नही दी होती है. वैसे स्थति में प्रश्न हल करने के लिए विशेष फार्मूला का प्रयोग किया जाता है. जो इस प्रकार है;
वर्ग का क्षेत्रफल – Area of Square in Hindi
सामान्यतः वर्ग का क्षेत्रफल मुख्यतः दो तरीकों से प्राप्त किया जाता है. पहला, यदि वर्ग की भुजा की लंबाई ज्ञात हो और दूसरा, अगर वर्ग के विकर्ण की माप ज्ञात हो. ऐसे स्थति में वर्ग का फार्मूला भिन्न-भिन्न होते है. हालांकि ये फार्मूला सरल है लेकिन इसका प्रयोग सावधानीपूर्वक करना अनिवार्य है.
1. वर्ग की भुजा ज्ञात होने पर:
यदि किसी वर्ग की प्रत्येक या किसी एक भुजा का लम्बाई ज्ञात हो, तो निम्न फार्मूला का प्रयोग किया जाता है.
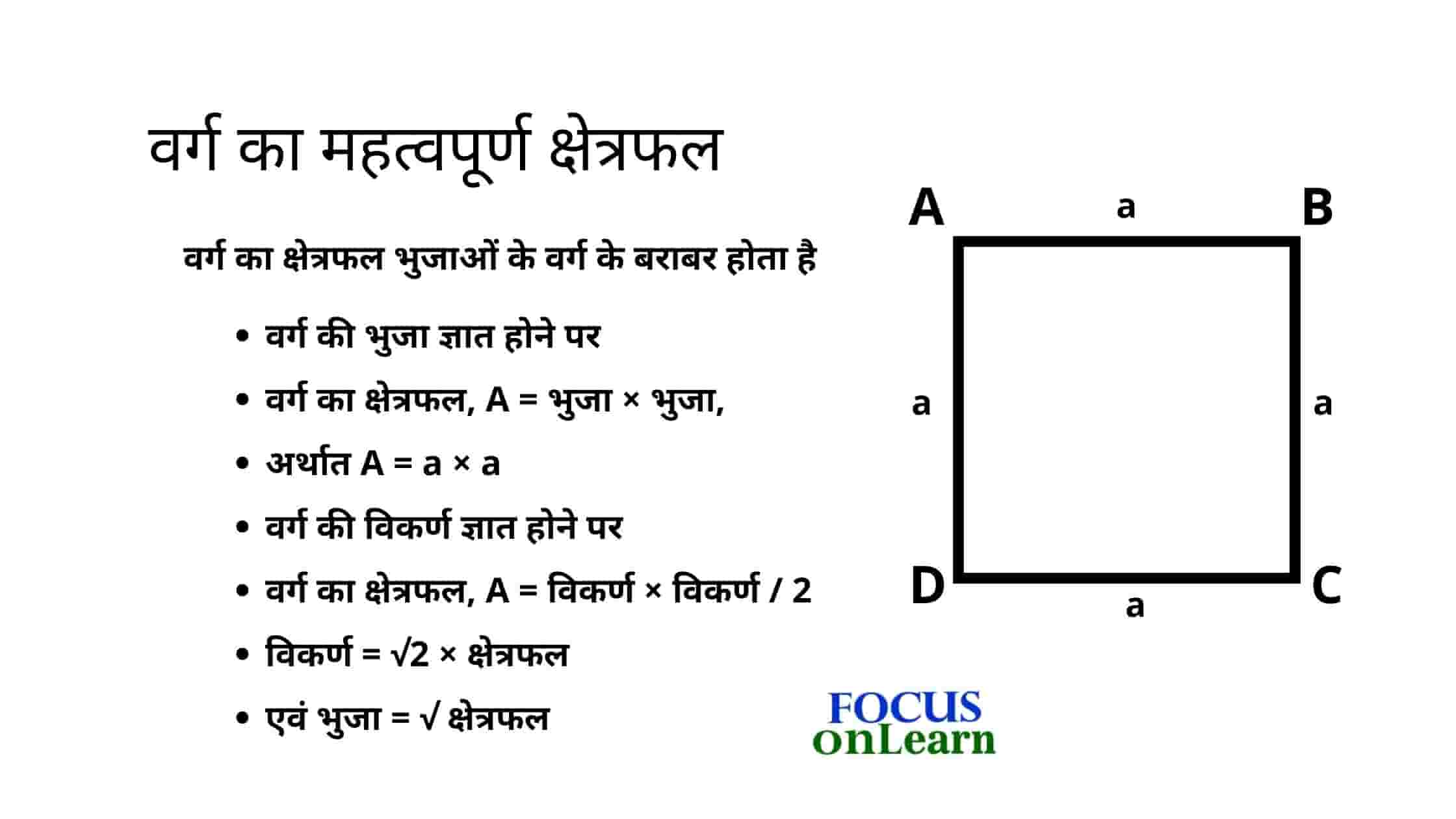
वर्ग का क्षेत्रफल, A = भुजा × भुजा, अर्थात A = a × a = a2
2. वर्ग की विकर्ण ज्ञात होने पर:
यदि किसी वर्ग का विकर्ण ज्ञात हो तथा क्षेत्रफल निकलना हो, तो निम्न फार्मूला का प्रयोग किया जाता है.
वर्ग का क्षेत्रफल, A = विकर्ण × विकर्ण / 2 अर्थात A = d2
जहाँ d = Diagonal, अर्थात विकर्ण है.
3. यदि क्षेत्रफल दिया हो, तो वर्ग का विकर्ण:
यदि किसी Varg Ka Kshetrafal दिया हो, तथा वर्ग का भुजा या विकर्ण ज्ञात करना हो, तो
विकर्ण = √2 × क्षेत्रफल
एवं भुजा = √ क्षेत्रफल
वर्ग का परिमाप = 4 × a
जहाँ a वर्ग के प्रत्येक भुजा की लम्बाई है.
अवश्य पढ़े, वर्ग का परिमाप एवं प्रयोग
Note: ऊपर दिए गए सभी वर्ग का क्षेत्रफल प्रतियोगिता और बोर्ड एग्जाम के दृष्टिकोण से आवश्यक है. अतः इन्हें स्मरण रखे.
वर्ग के क्षेत्रफल सम्बंधित तथ्य
- Varg की चारों भुजाएं आपस में समान होती हैं.
- वर्ग के प्रत्येक कोण 90 डिग्री के होते हैं.
- स्क्वायर के दोनों विकर्ण समान होते हैं.
- Square के चारों कोणों का योग 360 डिग्री के बराबर होता है.
- वर्ग के दोनों विकर्ण एक दूसरे को समकोण पर समद्विभाजित करते हैं.
- किसी वर्ग का क्षेत्रफल वर्ग का दोनो भुजाओं का गुणनफल होता है.
- एक वर्ग के विकर्ण की लम्बाई = √2 x भुजा होता है.
- जब वर्ग का क्षेत्रफल दिया हो, तो वर्ग की भुजा की माप = √क्षेत्रफल होता है.
अवश्य पढ़े, त्रिभुज के प्रकार और परिभाषा
वर्ग के क्षेत्रफल से सम्बंधित उदाहरण
1. यदि किसी वर्ग की प्रत्येक भुजा की लम्बाई 6 cm हो, तो वर्ग का क्षेत्रफल बताएं?
हल: दिया है, a = 6 cm
इसलिए, वर्ग का शेत्रफल = भुजा × भुजा
=> A = 6 × 6 cm2 => 36 cm2
2. एक वर्गाकार दिवार का लम्बाई 20 cm है, तो 2 cm2 के प्रति दर से उस दिवार को पेंट कराने की लगात ज्ञात करे?
हल: दिवार की लम्बाई 20 cm, अर्थात वर्ग की भुजा 20cm
=> A = भुजा × भुजा => 20 × 20 cm2 => 400 cm2
2 cm2 के दर से दिवार पेंट कराने में लगी कुल लागत = 400 × 2 = 800
महत्वपूर्ण तथ्य
वर्ग, चतुर्भुज का सबसे महत्वपूर्ण भाग है जो आयत, एवं समनान्तर चतुर्भुज के तरह कार्य करता है. अर्थात इसका गुणधर्म आयत एवं समनांतर समान होता है. लेकिन कई पहलुओं ये उनसे भिन्न है. अतः कंफ्यूज न हो. Varg Ka Kshetrafal का प्रयोग कई महत्वपूर्ण प्रशों को हल करने के लिए किया जाता है जो प्रतियोगिता एग्जाम में अधिक पूछा जाता है.
यहाँ केवल वर्ग का क्षेत्रफल से सम्बंधित फार्मूला का प्रयोग दर्शाया गया है जो गणितीय समस्या को हल करने में मदद करता है. यदि इससे सम्बंधित कोई समस्या हो, तो कृपया हमें कमेंट अवश्य करे.