गणित एक ऐसा विषय है जिसमे कैलकुलेशन की भागीदारी सबसे अहम होती है. और गणना करने के लिए भिन्न-भिन्न प्रकार के फार्मूला, नियम आदि का प्रयोग किया जाता है. गणित के अलग-अलग शाखा है जिसमे BODMAS Rule in Hindi का प्रयोग बीजीय निकाय को हल करने के लिए होता है.
BODMAS दरअसल सरलीकरण के अनुसार निर्देशित किया जाता है. अर्थात, BODMAS का प्रयोग सरलीकरण के लिए होता है जिसमे ब्रैकेट, ऑर्डर (का), भाग, गुणा, जोड़ और घटाव शामिल होते है. और इस गणना को BODMAS के नियम या रूल्स के अनुसार हल किया जाता है. क्योंकि, यह शुद्धता एवं स्पीड बढ़ाने में मदद करता है.
अंकगणितीय व्यंजक जिसमें जोड़, घटाव, गुणा, भाग आदि जैसे कई संक्रियाएं शामिल होते हैं, उन्हें दो संख्याओं वाले संक्रियाओं की तुलना में हल करना आसान नहीं होता है. इसलिए, BODMAS का प्रयोग कर उनका हल निर्धारित किया जाता है. अंकगणित में ऐसे कई स्टेज है जिसमे विभिन्न प्रकार के चिन्हों का प्रयोग प्रशों में किया जाता है. जो केवल और केवल BODMAS से ही हल होते है.
इससे सम्बंधित कई प्रश्न प्रतियोगिता एग्जाम में पूछे जाते है. इसलिए, आवश्यक है कि BODMAS के सभी नियम और प्रयोग विस्तार पूर्वक समझे और इसका प्रयोग प्रश्न हल करने में करे.
बोडमास नियम क्या है?
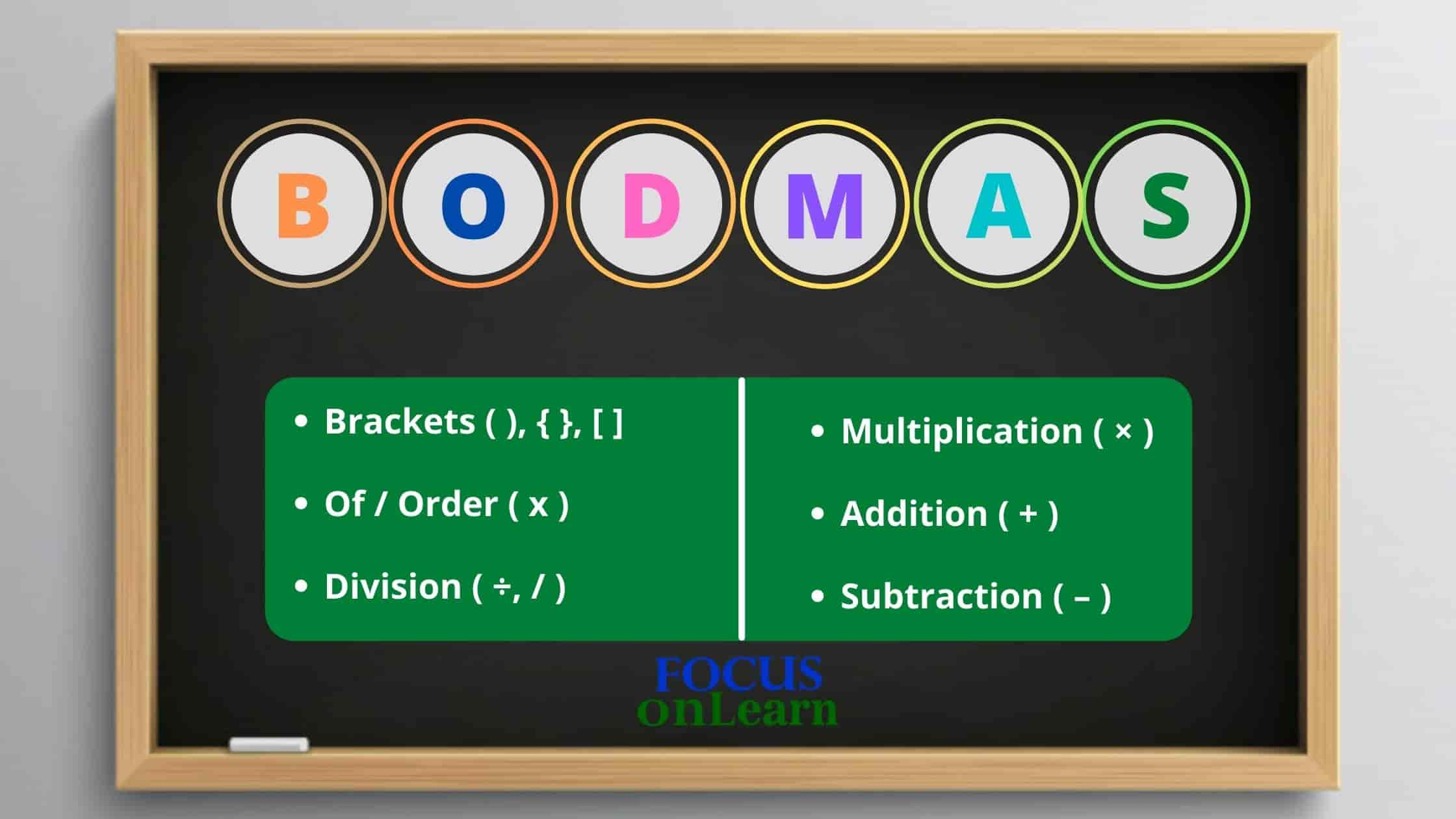
सामान्यतः BODMAS अंकगणितीय संक्रियाएँ करने का एक संक्षिप्त रूप है जिसमे ब्रैकेट, का (ऑर्डर), भाग, गुणा, जोड़ और घटाव शामिल है. अर्थात, BODMAS गणितीय संक्रियाएँ को सरल एवं उपयुक्त बनाने के लिए नियम प्रदान करता है, जिसके माध्यम से प्रश्न हल करना सरल हो जाता है.
गणित के विशेषज्ञ इसे PEMDAS भी कहते है क्योंकि यह BODMAS का ही एक synonym है. लेकिन यह अर्थ में BODMAS से बिल्कुल अलग होता है लेकिन प्रयोग एवं नियम के अनुसार बिल्कुल समान होता है.
यह यानि बोडमास व्यंजक को हल करते समय किए जाने वाले संक्रियाओं के क्रम की व्याख्या करता है, जिससे गणना करना सरल हो जाता है. यदि किसी अंकगणितीय व्यंजक में कोष्ठक जैसे ( ( ), { }, [ ] ) हैं तो पहले कोष्ठक को हल किया जाता है, उसके बाद विभाजन, गुणा, जोड़ और घटाव की संक्रियाएँ की जाती है.
| लाभ और हानि का फार्मूला | अलजेब्रा फार्मूला के सभी चार्ट |
| लघुगणक फार्मूला | हिरोन का फार्मूला |
| घन और घनमूल का सूत्र | चाल, समय और दुरी फार्मूला |
| अभाज्य संख्या | पूर्णांक संख्या |
BODMAS नियम कैसे कार्य करता है?
निचे दिए गए नियम पर बोडमास कार्य करता है. अतः स्मरण रखे.
बोर्ड मास का पूरा नाम क्या है?
बोडमास का पूरा नाम ब्रैकेट, ऑर्डर, डिवीजन, गुणा, जोड़, और घटाव होता है.
B = कोष्ठक ( Bracket )
- ― = रेखा कोष्ठक ( Line Bracket )
- ( ) = छोटा कोष्ठक ( Small Bracket or Circular Bracket )
- { } = मझला कोष्ठक ( Braces Or Curly Bracket )
- [ ] = बड़ा कोष्ठक ( Square Bracket Or Brackets )
O = का ( Of ) या घातांक ( Order )
- √ = वर्गमूल या घनमूल (Square root And Cube root)
- ( )2 और ( )³ वर्ग और घन (squire and cube )
D = भाग ( Division )
M = गुणा ( Multiplication )
A = योग ( Addition )
S = अन्तर ( Subtraction )
PEMDAS का रूल जो BODMAS का ही एक अलग रूप है.
- P = कोष्ठक (Parentheses)
- E = घातांक (Exponents)
- M = गुणा (Multiplication)
- D = भाग (Division)
- A = जोड़ (Addition)
- S = घटाव (Subtraction)
Note:- सबसे पहले Bracket की क्रिया उसके बाद OF (का) या घातांक, भाग, गुणा, जोड़, और घटाव की क्रिया प्रायः की जाती है.
BODMAS के प्रयोग पर प्रचलित कहावत
पहले ( का ) करो, पीछे ( भाग ) तब ( गुणा ) तब ( जोड़ ) एवं घटाव, अर्थात
- सर्वप्रथम कोष्टक
- इसके बाद “का” या “घातांक”
- फिर “Division” यानि ‘भाग’
- इसके बाद “Multiplication” यानी गुणा
- गुणा के बाद “Addition” यानी (जोड़)
- और सबसे बाद “Subtract”
BODMAS Rule पर आधारित उदाहरण
Examples हल करने के पहले कुछ points पर ध्यान देना आवश्यक है जो BODMAS Rule in Hindi के प्रयोग में सहायता करते है.
कोष्ठक इस क्रम जैसे (), { }, [ ] में हल किए जाते हैं. कोष्ठक हटाने का अर्थ है कोष्ठक के अंदर के व्यंजक को सरल करना.
यदि किसी कोष्ठक से पहले कोई संख्या है, तो कोष्ठक के अंदर उपलब्ध संख्या को उस संख्या से गुणा करके कोष्ठक को हटाया जाता है.
उदाहरण 1: [ 7 + 8 { 4 × ( 6 + 4 × 3 ) × 4}] को BODMAS Rule के मदद से हल करे?
हल: इस प्रश्न में ब्रैकेट, जोड़ और घटाव है. इसलिए, सबसे पहले ब्रैकेट्स को हल करते है.
[ 7 + 8 { 4 × ( 6 + 4 × 3 ) × 4}]
[ 7 + 8 { 4 × ( 6 + 12 ) × 4}]
[ 7 + 8 { 4 × 18 × 4}]
[ 7 + 8 { 4 × 18 × 4}]
[ 7 + 8 × 288]
[ 7 + 2304]
2311 (ans).
उदाहरण 2: (3 / 2 +5 / 3 ÷ 10 / 9 ) of (का) 5 / 12 का मान निकाले ?
हल: दिए गए प्रश्न “का”, ब्रैकेट्स, जोड़ और घटाव है. इसलिए, पहले “का” फिर ब्रैकेट्स को उसके बाद जोड़ और घटाव की संक्रिया करेंगे.
(3 / 2 + ( 5 / 3 ÷ 10 / 9 ) ) × 5 / 12
( 3 / 2 + ( 5 / 2 × 9 / 10 ) ) × 5 / 12
( 3 / 2 + 3 / 2 ) × 5 / 12
6 / 2 × 5 / 12
=> 5/4 (ans).
उदाहरण 3: 45 + 3 { 34 – 18 – 14 } ÷ 3 [ 17 + 3 × 4 – ( 2 × 7 ) ] का मान ज्ञात करे ?
हल: 45 + 3 { 34 – 18 – 14 } ÷ 3 [ 17 + 12 – 14 ]
[ 45 + 3 { 34 – 32 } ÷ 3 [ 17 + – 2 ] ]
[ 45 + 3 ( 2 ) ÷ 3 ( 15 ) ]
[ 45 + 6 ÷ 45 ]
677 / 15 (ans).
उदाहरण 3: ( 26 / 3 ) – ( ( 16 / 3 ) ÷ ( 8 / 3 ) ) + ( 1 / 3 ) को हल करे ?
हल: ( 26 / 3 ) – ( ( 16 / 3 ) × ( 3 / 8 ) ) + ( 1 / 3 )
( 26 / 3 ) – 2 + ( 1 / 3 ) [ LCM लेने पर ]
( 26 – 6 + 1 ) / 3
21 / 3
7 (ans).
महत्वपूर्ण तथ्य
गणित में कोष्ठकों का सरलीकरण BODMAS नियम द्वारा होता है जो प्रतियोगिता एग्जाम के लिए एक अहम भाग है. प्रत्येक वर्ष इससे प्रश्न पूछे जाते है. इसलिए, इसके नियमों को स्मरण रखना आवश्यक है. सामान्यतः BODMAS Rule in Hindi किसी भी बहु-संक्रिय ( अर्थात, ब्रैकेट, घातांक, भाग आदि) प्रश्न को हल करने का क्रम को निर्धारित करता है, जिससे गणना करना सरल हो जाता है.
BODMAS से सम्बंधित सभी आवश्यक तथ्य यहाँ उपलब्ध है जो प्रश्न हल करने में मदद कर सकते है. यदि इस टॉपिक में कोई संदेह हो, तो कृपया हमें कमेंट अवश्य करे.
अन्य गणितीय महत्वपूर्ण फार्मूला